Компьютерная томограмма зубов: описание и преимущества, схема проведения
описание и преимущества, схема проведения
1 августа 2017 Последняя редакция: 12 января 2020 Болезни зубов Автор статьи:В современной стоматологии пациентам нередко назначается компьютерная томография зубов. Многие пациенты находятся в недоумении, стоит ли проводить это исследование, не слишком ли оно рискованно и в каких случаях оправданно назначение КТ зубов.

В чем заключается томография зубов
При проведении любого вида КТ используется принцип разной проводимости лучей рентгена различными тканями организма: полостями, костями, мышцами, связками и др. При этом лучи проникают сквозь любые ткани организма и улавливаются с помощью специального детектора. После серии послойных снимков с помощью компьютера строится компьютерная томографическая 3D модель.
Чаще всего дентальная томография зубов назначается перед протезированием, имплантацией зубов, оперативным вмешательством на челюсть.
Метод рентгенографии не дает всех тех преимуществ, которые может дать метод современной компьютерной томографии. КТ зубов позволяет изучить различные особенности зубо-челюстной анатомии: строения зубов и каналов, состояние костей челюстей.
Результаты КТ незаменимы для ортопедов, детских стоматологов, ортодонтов, хирургов. Например, для наиболее точного изготовления любого протеза врачу часто необходимы данные о точных размерах челюстной анатомии максимально вех нюансах расположении зубов. Только в этом случае протез возможно изготовить с максимальной комфортностью для пациента.
Если при использовании имплантов вживление искусственного корня будет произведено неправильно (по неточным размерам или в неверно выбранном месте), то протез будет неудобным для пациента или быстро выйдет из строя.
Поэтому КТ во многих клиниках является обязательной подготовительной процедурой при любом виде зубного протезирования (съемные или дентальные протезы).
Незаменима томография зубов и для ортодонтов, так как идеально по
ᐈ КТ зубов | Цены от 1100 рублей
Общая информация
Компьютерная томография зубов – это обследование челюстно-лицевого аппарата, проводимая на томографе. Этот метод исследования является наиболее информационным и современным в стоматологии, предоставляет возможность осмотреть состояние зубов и челюсти.
Чаще всего диагностику назначают стоматологи и челюстно-лицевые хирурги перед проведением операции (имплантация, костная пластика).
Современное оборудование диагностирует все очаги деминерализации тканей зубов, что не представляется возможным сделать при обычном осмотре.
Что показывает?
Дентальная компьютерная томография визуализирует полость и пазухи носа, зубы, нижнюю и верхнюю челюсть. Констатирует следующие патологии:
- Воспалительное заболевание слюнной железы;
- Опухоль в зубочелюстном отделе;
- Воспалительное заболевание пародонта;
- Патологии корневого канала;
- Различные заболевания височно-нижнечелюстного отдела;
- Травмы;
- Инфекции;
- Абсцесс;
- Некроз;
- Зубо-десневые карманы;
- Аномалии зубов и их рост;
- Искривление перегородки;
- Не прорезавшиеся зубы.
Показания
КТ применяется при наличии следующих показаний:
- Травма;
- Проблемы в удалении зуба;
- Протезирование;
- Болевые ощущения в мышцах челюсти;
- Киста;
- Опухоль;
- Патология прикуса;
- Послеоперационный период;
- Предоперационное обследование;
- Аномалии роста зубов;
- Моделирование 3D;
- Контроль качества лечения.
Противопоказания
Противопоказаний к проведению исследования не так много:
- Беременность;
- Сахарный диабет;
- Некоторые проблемы с печенью и почками;
При проведении компьютерной томографии с введением контрастного вещества противопоказанием служит аллергическая реакция на йод, так как н содержится в контрасте.
С особой осторожностью к диагностике допускают пациентов с гиперкинезами, так как во время процедуры важно сохранять неподвижное положение. Движение в процессе обследования может смазать снимки.
Подготовка
Если планируется проведение компьютерной томографии зубов без введения контрастного вещества, то особой подготовки не требуется. Важно перед диагностикой оставить за пределами процедурного кабинета все металлические предметы: украшения, часы, ремень и прочие аксессуары.
В случае, если планируется пройти исследование с использованием контраста, то необходимо воздержаться от приема пищи в течение 6 часов до исследования. Вводят его при необходимости подтверждения новообразования в костях и мягких тканях лицевого отдела черепа, обнаружения опухоли и метастаз.
Как делают?
Проводится 3D КТ зубов либо сидя (стоя), либо лежа. В первом случае стоматологический компьютерный томограф (конусно-лучевой) выглядит, как ортопантограф и пациент в процессе диагностики стоит или сидит.
На шею и плечи накидывается специализированная ткань с прослойкой свинца. При этом необходимо подбородок зафиксировать на специальном месте для подбородка, а лбом упереться в фиксирующуюся опору.
Данную позу необходимо сохранить в течении 15-25 секунд, за этот период аппарат успеет сделать около 250 панорамных снимков зубов. Преобразование в 3D снимков займет ее пару минут. После чего пациент получает на руки полную информацию о состоянии зубочелюстной системы.
Во втором случае пациент ложится на подвижный стол томографа, принимает удобную позу. Голову фиксируют специализированными ремнями, после чего стол задвигается внутрь томографа и останавливается относительно области исследования. Кольцо начинает медленно вращаться, не создавая никакого дискомфорта пациенту.
Во время вращения датчики на кольце делают снимки, расстояние между которыми не превышает 0,1-0,2 мм. На весь процесс уходит около 10-15 минут.
Если компьютерная томография проводится с введением контрастного вещества, возможно появление в ротовой полости неприятного привкуса и тошноты. При этом время на проведение увеличивается в 2 раза (около 20 минут).
Видео о том как проходит процесс диагностики:
Вредно ли КТ зубов?
Компьютерная томография проводится при использовании рентгеновских лучей. Лучевое воздействие на организм человека минимальное (0.039 – 0,06 мЗв), поэтому оно не оказывает никакого отрицательного воздействия. Благодаря минимальному излучению процедура не противопоказана даже детям.
Можно проходить 3D компьютерную томография зубов 8-10 раз в год. Именно это количество процедур не превышает допустимую норму излучения в год.
При дентальной КТ зубов пациент получает исключительно достоверную информацию, на основе которой в дальнейшем составляется план лечения.
Что такое 3D-снимок зубов
3 D изображение зуба – результат компьютерной томографии. Относится к группе инновационных изобретений, однако уже стало популярным. С помощью этой формы диагностики стоматолог получает трёхмерное изображение челюсти с подробным отображением всех деталей. Благодаря этому врач в любой момент может изучить зубы пациента под удобным ракурсом.
Аналог 3D-диагностики – ортопантомограмма (ОПТГ) – панорамный снимок челюсти. Однако он, в отличие от объёмной модели, является отображением зубов в двухмерной плоскости. Главный минус метода – снимок имеет значительные искажения, и стоматолог может неправильно интерпретировать ОПТГ.
3D-снимки лишены этого недостатка. Напротив, даже при формировании на основе объёмной модели среза зуба врач получает точное изображение, полностью имитирующее реальную «обстановку». 3D-модель позволяет оценить состояние зубов, дёсен, костной ткани, увидеть имеющиеся проблемы.


Благодаря внедрению этого метода стоматологи смогли значительно повысить результативность своей работы. Риск задеть здоровые участки либо не до конца устранить новообразования, наоборот, значительно снизился.
Какая рентгеновская аппаратура нужна
Рентгеновский 3D-снимок челюсти выполняется с помощью компьютерного томографа. Это современная цифровая аппаратура, которая обеспечивает качественную диагностику при минимальном облучении пациента. Для получения точного изображения к томографу подключены сверхчувствительные детекторы.
Чтобы перенести полученные данные в компьютер и создать объёмную модель, необходимо специальное программное обеспечение.
Отталкиваясь от сложности заболевания и нужной точности снимка, делается многослойное исследование. В результате врач получает до 10 проекций человеческой челюсти.
Показания к проведению данного вида обследования
3D-снимок для исследования зубов применяется при диагностике сложных травм и заболеваний челюсти. К показаниям для назначения компьютерной томографии относятся:
- неправильное расположение зуба в десне;
- новообразования в гайморовых пазухах либо челюсти;
- обширный воспалительный процесс;
- неправильный прикус;
- нарушения двигательных функций нижнечелюстного сустава;
- сложности при имплантации и протезировании;
- переломы нижней челюсти;
- диагностика кариесных осложнений;
- планирование ортопедического лечения и оценка его результатов;
- планирование цефалометрических изменений;
- диагностика пародонтита.
Основные противопоказания
3D компьютерная томография зубов основывается на рентгеновском излучении, поэтому нельзя назвать эту процедуру полностью безопасной. Лучевая нагрузка в процессе этого обследования составляет от 0,045 до 0,06 мЗв. Это не очень высокий показатель, учитывая, что годовой предел облучения составляет 5 мЗв (согласно Минздраву РФ).
Что же касается противопоказаний, то они стандартные для всех видов рентгенологических обследований. Основное ограничение – это период беременности (особенно в первом триместре). В данном случае, ситуация рассматривается в индивидуальном порядке, исходя из соотношения вреда для ребенка и пользы для матери.
Если используется контрастное вещество (в КТ зубов и челюсти применяется не так часто), то к числу противопоказаний можно добавить:
- Пациенты, страдающие от заболеваний щитовидной железы.
- Почечная недостаточность.
- Аллергия на препараты, содержащие йод.
Лактационный период не является противопоказание, но после процедуры должно пройти не менее 48 часов до следующего кормления грудью.
Можно ли делать детям?
Многие родители думают, что использование 3D компьютерной томографии невозможно в детском возрасте по причине негативного влияния на организм ребенка. Это не совсем так, ведь особое внимание к данному исследованию отдается именно в педиатрии.
Если соблюдать все правила безопасности и не превышать периодичность процедур (для детей – 1 раз в год), то обследование не приведет к каким-либо патологическим изменениям в детском организме.
3Д КТ в детской стоматологии позволяет оценить состояние носовых пазух, десен и увидеть зачатки молочных зубов. Также этот метод позволяет выявить патологии прикуса у ребенка.
Как подготовиться к исследованию
Специальной подготовки к исследованию не требуется. Перед процедурой стоматолог просит снять украшения и убрать различные предметы, которые могут помешать сканированию. При наличии во рту ортопедических конструкций с металлическими элементами их придется убрать.
Перед самой процедурой рентгенолог надевает на пациента специальный фартук, закрывающий грудную клетку и живот. Важным моментом исследования будет и то, кто его проводит. Не исключены ситуации, когда в клиниках вместо рентгенолога работает обычная медсестра, потому не лишним будет спросить у специалиста удостоверение о повышении квалификации в области рентгенографии.
Сколько длится по времени?
Длительность зависит от типа томографа. Основная рекомендация в этом вопросе — перед исследованием поинтересоваться типом устройства и выбирать клинику с максимально современным аппаратом высокой мощности. Его преимущества — не только минимальная доза облучения и высокая детализация, но и намного меньшее время проведения исследования. Для сравнения, продолжительность сканирования может варьироваться от нескольких секунд до 15 минут.


Возможный вред
Конусно-лучевая дентальная компьютерная томография – это самый безопасный и быстрый метод диагностики. Благодаря использованию рентгеновского луча конической формы, получаемая в процессе исследования доза излучения, в 10 раз меньше, чем при использовании спиральной КТ. А пульсирующий режим рентгеновского луча дополнительно снижает дозу облучения. Трехмерный компьютерный томограф SOREDEX Scanora 3D, относится к наиболее безопасным по дозе рентгеновского облучения аппаратам – всего 0,035 м3в.
Однако, несмотря на безопасность исследования, у КТ есть и противопоказания. Если говорить просто о томографии зуба, она не проводится при беременности (в 1 триместре). 3d рентген зубов с контрастом запрещен беременным и кормящим женщинам, пациентам с эндокринными нарушениями (сахарный диабет, патологии щитовидной железы), почечной недостаточностью и непереносимостью йодсодержащих препаратов.
Преимущества метода
- Возможность повернуть, увеличить, исследовать снимки в любой проекции и сечении, что невозможно при обычном 2-х мерном сканировании.
- Обследование длится всего несколько секунд (8-20 секунд).
- Полная диагностическая информация.
- Максимальная безопасность.
- Цифровой формат информации.
- Обнаружение любых патологических процессов на ранней стадии.
- Не требуется предварительная подготовка.
- Трехмерная реконструкция без искажения и артефактов.
- Широкий спектр назначений – от эндодонтического лечения зубов и имплантации, до челюстно-лицевых операций.
Есть ли альтернатива КТ


Существует множество других способов диагностической визуализации (рентгенограмма, ортопантомограмма, УЗИ и т.д.), но лишь КТ предоставляет возможность высокоточного, раздельного изображения всех типов ткани под разным углом и на разную глубину. Хотя панорамный снимок зубов и сегодня остается не менее важным диагностическим инструментом стоматолога, он может предоставить только общую обзорную картину. В свою очередь, 3d томограмма позволяет получить не единственный плоский снимок челюсти, а целый ряд последовательных многоплоскостных изображений в различной проекции и без искажений, присущих панорамному снимку.
Пример:из-за разной плотности костных структур, попавших в действие рентгеновского излучения, на 2-х мерном изображении невозможно рассмотреть менее плотную кость, точную информацию предоставляет 3d снимок зубов.
Что лучше — панорамный или 3D снимок
Отличием КТ от стандартной ортопантомограммы будет получение трехмерного изображения. Такой вариант диагностики более результативный, но в некоторых случаях в этом нет необходимости. Ортопантомограмма бывает аналоговой и цифровой. Последняя отличается более высоким качеством, и снимки можно сохранить на различные носители. Также эта процедура отличается скоростью, ведь весь процесс сканирования занимает несколько секунд.


Стандартная ортопантомограмма
Панорамный снимок можно делать всем, включая маленьких детей, но нечасто. Более того, именно для ребенка он имеет первостепенное значение, ведь это помогает визуализировать зубной ряд для предупреждения проблем с прикусом и ранней диагностики заболеваний.
Как проходит процедура и расшифровка


Чтобы сделать 3D снимок зубов, стоящему или сидящему пациенту необходимо закусить специальную пластину и зафиксировать свое положение в аппарате с помощью фиксирующей стойки. В течение всего времени сканирования нужно соблюдать абсолютную неподвижность.
Сенсор томографа на протяжении 8-20 секунд совершает ряд оборотов вокруг головы пациента, производя около 200 снимков в разных проекциях. Обработка цифровых данных занимает 5-15 минут после чего информация записывается на диск или флеш-накопитель. Никакой подготовки не требуется, нужно лишь снять перед процедурой все металлические украшения с шеи, ушей, волос.
Как выглядит снимок
Полученные при обследовании данные имеют вид множества проекций. Для создания объёмной модели компьютерная программа собирает их в отдельное целое. Если дальнейшая диагностика проходит в кабинете, оснащённом компьютерной техникой, врач открывает снимок в электронном виде с цифрового носителя. Последний выдаётся пациенту после проведения томографии. Для более полного ознакомления с проблемой стоматолог может покрутить модель, найдя интересующую область, а также вывести на экран соответствующую проекцию зубов. Онлайн доступны увеличение мелких элементов, создание срезов, проведение необходимых замеров и прочие операции.
Врач может запросить напечатанный снимок объёмной модели челюсти. В этом случае пациенту выдают на руки изображение в формате 8×5 либо 5×5 см. На них запечатлеются до десятка основных проекций и сечений. Этот вариант считается менее удобным при диагностике и используется преимущественно в кабинетах, не оборудованных компьютерной техникой.


Что можно обнаружить
3D-рентген зубов даёт возможность получить следующую информацию:
- визуализация состояния зубов и дёсен в трёхмерной модели;
- наличие и размеры очагов патологий;
- эффективность лечения либо хирургического воздействия;
- расположение, характер и размеры новообразований, кист и других опухолей;
- определение основных параметров челюсти и её геометрии;
- графическая фиксация расположения нервов;
- подсчёт количества костной ткани.
Особенности применения КТКЛ в стоматологии
В стоматологической практике конусно-лучевая томография челюсти применяется для решения сложных задач:
- удаление корней или «восьмерок»;
- извлечение инородного тела, обломка;
- обследование каналов;
- исключение новообразований челюсти;
- выявление деструкции костной ткани;
- оценка периапикальных тканей дентина зубов;
- обнаружение аномалий и врожденных дефектов;
- подготовка к установке импланта.
Обследование остается единственной диагностикой в стоматологии, позволяющей правильно оценить положение каналов, состояние пульпы, наличие нервных окончаний. Это важная часть обследования перед сложнейшими операциями на надкостнице, вживлению остеопротеза.
Благодаря высокой результативности в несколько раз уменьшается риск отторжения металлического штифта и других осложнений. Преимущества КЛКТ челюсти перед другими методиками:
- Комфорт для пациента, отсутствие неприятных ощущений, что немаловажно для людей, которые с боязнью идут к стоматологам.
- Минимальные затраты времени на качественное обследование, что сокращает количество посещений стоматологического кабинета.
- Для обследования зубных каналов применение КЛКТ является единственной возможностью вымерять длину. Врачу легче подобрать идеальную форму пломбы или штифта.
Кроме изучения состояния зубов и костей, КЛКТ позволяет осмотреть мягкие ткани. Это помогает своевременно обнаружить кисту в корне моляра, свищ или онкологическую опухоль в полости рта, подобрать лечебные средства. Полученные данные в последствие используются при подготовке операции. Стоматологи могут составить визуальную модель и показать пациенту, как будет выглядеть лицо после проведения всех процедур, убедиться в оптимальной форме коронок.
Доза облучения исследования
Многие люди задаются естественным вопросом, какова доза получаемых облучений у конусно-лучевой компьютерной томографии. У данного метода исследования нагрузка рентгеновскими лучами гораздо ниже, чем при обследовании спиральной томографией. Это связано с высокой скоростью вращения трубки. Тем не менее не следует самому себе назначать данную диагностику, поскольку только врач может оценить действительную необходимость ее проведения.
К тому же следует учитывать следующие факторы:
- проведение обычной флюорографии дает облечение 0,18 мЗв;
- от естественного фона Земли каждый человек получает радиацию около 1000 мкЗв;
- предельно допустимой дозой, при которой не происходит существенных изменений человеческого организма является 5000 мкЗв.
В связи с коротким временем проведения обследования, у конусно-лучевой компьютерной томографии лучевая нагрузка находится в пределах 40–120 мЗв. Если провести исследование черепа спиральной компьютерной томографией, то лучевое воздействие увеличится от 400 до 600 мЗв. Кроме того, проведение проверки на конусном-лучевом томографе позволяет исключить дальнейшее обследование при помощи других диагностических методик, то получается невысокой общая лучевая нагрузка на организм исследуемого.
Где применяется исследование
Принцип действия конусной-лучевой компьютерной томографии основан на визуализации обследуемой зоны. Данный аппарат не только отличается возможностью получения трехмерной модели проблемной зоны, но и своей компактностью, безопасностью. Впервые исследования на нем начали производиться в США, затем попали в Европу.
Современные аппараты оснащены роботизированной рукой, позволяющей выбрать нужную траекторию для задачи движений датчика. В основном они позволяют проводить обследование на небольшой по размеру области, но, если имеется необходимость, то для расширения объема используется функция склеивания.
Этот вид томографии широко используется для выявления проблем в следующих сферах стоматологического исследования:
- Терапевтической стоматологии позволяет выявить острые воспалительные процессы не только зубов, но и окружающих их мягких тканей. Используется для исследования каналов, распознавания области разрушения корня зуба, контроля терапии.
- Хирургической стоматологии позволяет определить местонахождение воспаления, его размер, место забора кости для имплантата. Применяется для обнаружения патологий, образовавшихся в результате низкокачественной терапии, хирургического вмешательства, позволяет обнаружить оставшиеся после удаления части зуба.
- В ортопедии позволяет точно составить план лечения, оценить состояние опорного зуба, своевременно выявить осложнения, развивавшиеся из-за установления конструкции.
- В ортодонтии используется для планирования, позволяет правильно принять решение о необходимости устранения зубов, которые мешают установить конструкцию протеза.


Современный метод исследования позволяет доктору получать результаты на свой компьютер
Широко известно применение конусно-лучевой компьютерной томографии не только в стоматологии, но и для решения проблем:
- в имплантологии позволяет подготовить пациента к имплантации, оценить состояние костей, получить точные сведения о месте, в котором предполагается проведение манипуляции;
- ЧЛХ используется для оценивания травмирования кости, обнаружения опухолевых новообразований, терапии воспалений;
- оториноларингологии позволяет оценить состояние полости носа, его пазух, принять правильное решение о целесообразности проведения операций, контролировать и корректировать лечение.
Данные направления имеют небольшую область сканирования, обычно это оценка состояний челюстных костей, носовой перегородки, мягких, костных тканей черепной коробки. Чаще всего этот метод используется для диагностирования врожденных патологий неба, подбора имплантатов, исследования болезней носовых пазух, аномальных расположений зубов, когда другие методы не дают возможности выставления точного диагноза.
Ограничения для проведения исследования
Хотя метод конусно-лучевой компьютерной томографии считается инновацией, позволяющей точно определить состояние исследуемой области, необходимо учитывать, что он относится к разряду радиационных методик и поэтому требует некоторой осторожности. Прежде всего его ограниченно назначают:
- для детей, не достигших 5-летнего возраста. Для данной категории населения этот метод исследования может назначаться лишь при наличии жизненных показаний;
- лиц, страдающих почечной недостаточностью;
- людей, которые не могут находиться в неподвижном состоянии на протяжении 2–3 минут;
- пациентов, которые имеют ярко выраженный болевой синдром;
- беременных женщин.
В период беременности противопоказано проведение любой томографии и рентгенографии. Исключением является лишь жизненная необходимость для получения срочной медицинской помощи, при условии, что польза от обследования для матери будет ниже предполагаемого риска для плода. Кроме того, следует обсудить с врачом подготовку, позволяющую снизить риск негативного воздействия рентгеновскими лучами.
Проведение процедуры в третьем или втором триместре дает меньшую вероятность развития патологий у плода. Для проведения конусно-лучевой томографии требуется назначение лечащего доктора, который сможет адекватно оценить все риски для организма от данного исследования.
Исследование детей
Бывают случаи необходимости проведения данного исследования детям младшего возраста. Конечно, детский организм более чувствителен к радиации, но при наличии серьезных показаний от диагностики не следует отказываться. Если же у ребенка нет наличия абсолютного противопоказания к исследованию, то данный метод может применяться даже для малышей первого года жизни.
К таким ограничениям относятся:
- родовая травма;
- врожденные аномалии;
- аллергические реакции на препараты, используемые для дачи наркоза;
- порок сердца.


Дети старшего возраста довольно легко переносят данное обследование
Перед тем как проводить обследование детям, их не следует кормить на протяжении 2,5 часов до предполагаемой процедуры, иначе может сформироваться аспирационная пневмония. Когда же на момент исследования ребенку уже исполнилось 4 года, то следует с ним поговорить. При этом постараться объяснить ход проведения процедуры, обязательно акцентировать внимание, что мама и папа будут все время находиться рядом.
Деткам более младшего возраста исследование проводится под наркозом. Причем во время диагностики родители могут находиться вместе с крохой и с надетыми на себя для защиты свинцовыми фартуками.
Описание диагностической процедуры
Чтобы понять, как делают компьютерную томографию, стоит рассмотреть поэтапное описание процесса:
- непосредственно перед процедурой специалист попросит снять все металлические украшения, чтобы избежать сбоев в работе оборудования,
- далее пациент надевает специальный защитный жилет, чтобы снизить степень облучения организма в целом,
- пациент становится или присаживается спиной к аппарату, а его подбородок фиксируется с помощью специальной подставки – это необходимо, чтобы исключить лишние движения и получить максимально точно изображение,
- после включения аппарата вокруг головы пациента начинает вращаться сканер с излучающей трубкой – именно он передает трехмерное изображение на компьютер.


На фото изображено выполнение томографии
Процедура длится меньше минуты. Диагностика совершенно безболезненная, не требует от пациента какой-либо серьезной подготовки.
Как часто можно повторять процедуру
Многих волнует вопрос о том, вредно ли проходить томографию и как облучение отражается на здоровье организма в целом. Волноваться по этому поводу не стоит, поскольку доза облучения конусно-лучевого томографа очень мала и не несет никакой опасности для здоровья пациента. Проходить процедуру разрешается до 12-14 раз в год1.
Так, если сравнить с прочими методиками рентген-диагностики, то одна спиральная КТ черепа соответствует примерно 2000 прицельным снимкам. Облучение при прохождении флюорографии в 2-3 раза выше, чем при КТ обеих челюстей. Максимально допустимая лучевая нагрузка в течение года для взрослого человека составляет 1000 мкЗв, а для детей в возрасте до 15 лет – 300-400 мкЗв. Во время проведения диагностики обеих челюстей нагрузка составляет всего 70 мкЗ, поэтому повторять процедуру можно до 14 раз в течение года.
Источники:
- https://iDiagnost.ru/kt/podgotovka-i-provedenie-3d-snimkov-zubov
- https://Center-Luch.ru/stati/3d-snimok-zubov/
- https://zub.clinic/protezy/3dkt
- https://dental-clinic.expert/3d-kompyuternaya-tomografiya-zubov/
- https://simpladent.com/publication/dlya_pacientov/3d-snimok-zubov/
- https://mrtdom.ru/diagnostika-kt/kt-golovy/klkt-v-stomatologii
- https://apkhleb.ru/kt/konusno-luchevaya-kompyuternaya-tomografiya
- https://DentConsult.ru/lechenie-zubov/kompyuternaya-tomografiya-zubov-i-chelyu.html
Екатерина Беликова
Врач-стоматолог-терапевт. Пародонтолог. Врач высшей категор. Специалист высокого класса. Специализируется на лечении кариозных и не кариозных поражений зубов.
 Шоссе Революции, 18к2 Шоссе Революции, 18к2 Адрес: Красногвардейский район, 195176, Санкт-Петербург, шоссе Революции, дом 18, корпус 2 | |
 Улица Оптиков, 45к1 Улица Оптиков, 45к1 Адрес: Приморский район, 197082, Санкт-Петербург, улица Оптиков, дом 45, корпус 1 | |
 Фронтовая улица, 3У Фронтовая улица, 3У Адрес: Петродворцовый район, 198515, Санкт-Петербург, поселок Стрельна, Фронтовая улица, дом 3У | |
 Ростовская улица, 13-15 Ростовская улица, 13-15 Адрес: Пушкинский район, 196634, Санкт-Петербург, поселок Шушары, микр. Славянка, Ростовская улица, дом 13-15 | |
 Улица Асафьева, 7к1 Улица Асафьева, 7к1 Адрес: Выборгский район, 194356, Санкт-Петербург, улица Асафьева, дом 7, корпус 1 |  Центральная улица, 54к2 Центральная улица, 54к2 Адрес: Всеволожский район, 188691, Ленинградская область, город Кудрово, улица Центральная, дом 54, корпус 2 |
 Всеволожский проспект, 68 Всеволожский проспект, 68 Адрес: Всеволожский район, 188640, Ленинградская область, город Всеволожск, Всеволожский проспект, дом 68, корпус 1 | |
 Проспект Ленина, 53 Проспект Ленина, 53 Адрес: Колпинский район, 196650, Санкт-Петербург, город Колпино, проспект Ленина, дом 53 |  Проспект Ленина, 59 Проспект Ленина, 59 Адрес: Красносельский район, 198320, Санкт-Петербург, город Красное Село, проспект Ленина, дом 59 |
Что такое томография зубов
Томография — это метод исследования, при котором врач может получить послойное изображение того или иного органа. Проводится это обследование с помощью специального аппарата — томографа. Полученные данные передаются на компьютер, который обрабатывает их и выдает на экран изображение. Какие виды томографии зубов существуют:
- Самый распространенный метод — это классическая компьютерная томография. Изображение при этом получается двухмерным и плоским. Его можно распечатать на специальной бумаге.
- Более современная методика — это 3Д-томография. С ее помощью можно получить трехмерное изображение, которое можно изучать только на экране компьютера.
Что такое 3D-томография
3Д-томографией в медицине называют такой диагностический метод, который позволяет оценить состояние исследуемого органа со всех сторон — в трех проекциях. Используется этот способ и в стоматологии — компьютерная томография зубов.
Благодаря этому методу можно исследовать состояние ротовой полости, челюстей и зубов в отдельности наиболее полноценно. 3D-томография зубов является более качественным и информативным методом диагностики, чем обычная рентгенография. Результат, полученный при исследовании, называется ортопантомограммой, или конусной томограммой.
Техника проведения
Проводится это исследование с помощью специального аппарата — стоматологического томографа. Он подключен к компьютеру, и вся информация, полученная при исследовании, переносится в него. Там она обрабатывается в цифровое изображение — объемную трехмерную модель ротовой полости пациента. Аппарат для проведения процедуры может быть спиральным или мультиспиральным.
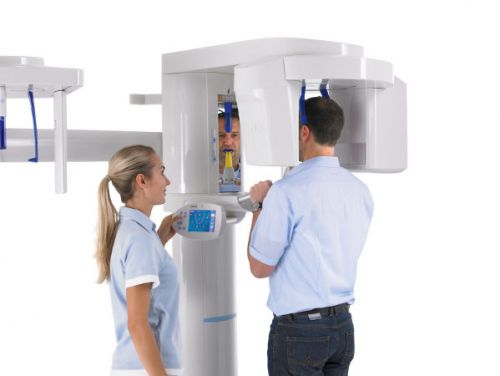
Для проведения исследования пациенту предлагают поставить подбородок на подставку, а вокруг его головы будет вращаться основная часть аппарата
Благодаря тому, что вся информация хранится в компьютере, томограмму можно пересматривать в любое время. Также существует возможность предварительно оценить ход оперативного вмешательства — если оно требуется. С помощью специальных программ можно рассчитать все ходы операции и смоделировать желаемый конечный результат. Также этот результат можно использовать в различных консилиумах — в трудных диагностических вопросах.
Так как исследование длится всего несколько секунд, доза рентгеновского облучения сведена к минимуму — это преимущество перед обычным рентгеном. Пациенту предлагают установить подбородок на специальную подставку, а лбом прижаться к стойке аппарата. Между зубов помещается пластина. Во время исследования вокруг головы пациента вращается часть аппарата, осуществляющая множество снимков. Такое большое количество одномоментно сделанных снимков и позволяет создать трехмерное изображение. За все время исследования аппарат делает около 200 изображений.
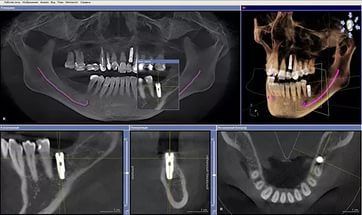
На снимке можно увидеть все зубы, челюсти и оценить состояние пародонта
Если требуется получить большую четкость изображения или при подозрении на наличие полостей внутри челюсти, исследование проводится с использованием контраста. Еще один плюс исследования в том, что оно может проводиться неоднократно за малые промежутки времени. Это необходимо при длительном лечении тяжелых заболеваний, например, опухолевых.
Показания
Для проведения компьютерной томографии зубов определен ряд показаний. Хотя это исследование может проводиться и по желанию пациента, на сегодняшний день оно является достаточно дорогостоящим и в государственных учреждениях проводится только по строгим показаниям. Частные клиники могут делать томографию в любом случае — так повышается диагностическая ценность исследования.
Какие показания существуют для проведения 3D-томографии?
- Диагностическое исследование при заболеваниях, которые не могут быть установлены при стандартных методиках.
- Подготовка к оперативному вмешательству.
- Подготовка к имплантации зубов.
- Детская стоматология — когда требуется провести исправление прикуса.
- Диагностика и лечение травматических повреждений.
- Определение скрытого кариеса.
- Диагностика зубов мудрости.
Что можно увидеть
С помощью дентальной томографии можно обнаружить различные, даже самые мельчайшие патологии в ротовой полости. Что позволяет увидеть этот диагностический метод?
- различные травмы челюстей и зубов;
- дефекты в развитии зубов, десен и костной основы челюсти;
- можно оценить положение зубов относительно друг друга и расположение их в десневых карманах;
- оценивается состояние носовых пазух и выстилающей их слизистой;
- очаги хронической инфекции в самих зубах, мягких тканях и костях челюсти.
Также зубная томография помогает в лечебных мероприятиях:
- определение объема предстоящего оперативного вмешательства;
- подготовка к сложной операции по удалению зубов или их протезированию;
- отслеживание развития злокачественных новообразований в ротовой полости или в зубной челюсти.
Какие разделы стоматологии пользуются этим методом исследования?
- Эндодонтология — оценка состояния зубной полости, корневых каналов, пульпы зуба.
- Хирургическая область стоматологии — подготовка к оперативному вмешательству, оценка результатов лечения, контроль заживления.
- Пародонтология — занимается диагностикой и лечением заболеваний пародонта (склеротические изменения, опухоли, остеопороз).
- Ортодонтия — занимается оценкой состояния зубов, костных структур десен, прикусом.
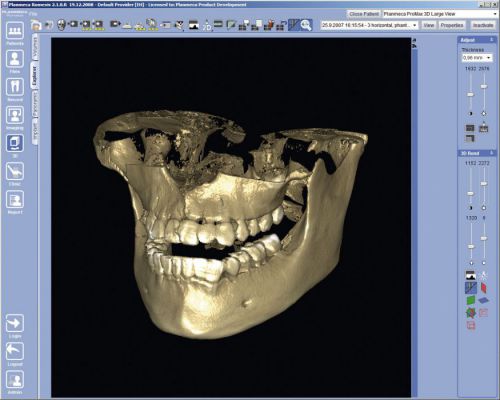
Компьютер обрабатывает данные и выводит их на экран в виде трехмерного изображения
Подготовка и противопоказания
Единственным противопоказанием к проведению этого исследования является беременность — на любом сроке. Возрастных ограничений для проведения исследования нет.
Если используется контраст во время исследования — добавляется еще одно противопоказание. Это люди с тяжелыми заболеваниями мочевыводящих путей, поскольку контраст выводится из организма через почки.
Не прямым противопоказанием является клаустрофобия — угрозы для жизни таких пациентов исследование не несет, но им становится некомфортно во время вращения аппарата.
Специальная подготовка к проведению исследования не требуется. Пациента лишь просят перед процедурой снять все металлические предметы. Для защиты от рентгеновского излучения надевается специальный жилет со свинцовой прослойкой.
Сделать томограмму зубов в трехмерной проекции можно в частных клиниках или в государственных учреждениях по показаниям.
КТ зубов — это аппаратный метод диагностики, который позволяет точно исследовать ткани полости рта. В сущности, он представляет собой усовершенствованный рентген, только обычная ортопантомограмма дает двухмерный, «плоский» снимок, а компьютерная томография позволяет получить точное трехмерное цифровое изображение.
Благодаря томографии зубов врач-стоматолог получает исчерпывающую информацию о состоянии зубочелюстной системы пациента. В связи с этим она применяется очень широко для решения множества задач:
- оценки структуры, особенностей строения, состояния и степени изменений тканей;
- точной диагностики причины определенных симптомов;
- контроля эффективности принятых мер или проведенного лечения.
Это делает метод востребованным в терапевтической, хирургической стоматологии, имплантологии и пародонтологии. При необходимости проведения терапевтического лечения томограмма дает возможность оценить однородность пломбировочного материала, увидеть количество и структуру корневой системы, каналов. Хирургическая стоматология и имплантология использует КТ для оценки костной ткани, в том числе ее плотности.
Компьютерная томография зубов также позволяет точно определить очаги воспаления, обнаружить перегородки и иные особенности.
Кому показана и противопоказана КТ
Показаниями к выполнению томограммы выступают следующие:
- подготовка к имплантации или составление плана лечения перед протезированием, сложным хирургическим вмешательством или осложненным удалением зубов, ортодонтическим лечением;
- травмы: ушибы, переломы корня или подозрения на них, иные механические повреждения;
- дефекты, врожденные аномалии развития челюстей;
- нарушения прикуса, необходимость в точном определении количества зачатков зубов, оценке направления их прорезывания и пр.;
- болезни десен и тканей пародонта;
- подозрение на глубокий кариес, пульпит, пародонтит, кисту корня зуба и т.д.;
- эндодонтическое лечение — КТ позволяет спланировать его и впоследствии оценить эффективность и правильность пломбирования каналов;
- подозрения на опухоли костных структур;
- необходимость оценки состояния верхнечелюстных пазух, височнонижнечелюстных суставов для правильного составления схемы терапии и др.
Снимок КТ зубов является безопасным, и его не рекомендуют проводить только беременным. Впрочем, если потенциальная польза от постановки точного диагноза превышает вероятные риски, иногда выполнение томограммы целесообразно. К относительным или косвенно относящимся к методу противопоказаниям относят психические заболевания, клаустрофобию. Метод не подходит пациентам, которые не могут находиться в неподвижном состоянии в течение определенного времени. Однако если допускается применение седативных средств, это существенно облегчает диагностику.
Преимущества метода
Дентальная компьютерная томография является одним из наиболее эффективных методов диагностики. Она характеризуется несколькими преимуществами:
- информативность — врач получает возможность оценить ткани всесторонне, можно исследовать участки под различными углами, в любой из плоскостей, детализировать изображение. Это помогает поставить правильный диагноз;
- скорость проведения процедуры — «картинку» можно получить за считанные секунды;
- безболезненность — целостность тканей не нарушается, сама процедура не доставляет дискомфорта;
- низкая лучевая нагрузка — минимально возможная нагрузка не оказывает влияния на здоровье даже при необходимости проведения серии снимков в течение короткого промежутка времени;
возможность оперировать данными обследования — их можно записать на электронный носитель или отправить по почте.
Сделать КТ зубов в СПб вы можете в ГК СТОМА. Современное оснащение оборудованием — аппаратом PLANMECA PROMAX 3D, а также современным программным обеспечением позволяет нам оказывать качественные диагностические услуги. Они являются залогом правильного плана лечения, достижения желаемых результатов наиболее оптимальным путем, исключения вероятности ошибки. Уточнить цену КТ зубов, записаться на обследование вы можете, заполнив специальную форму на сайте или позвонив нам.
90000 Computed Tomography (CT) 90001 90002 Breast CT scanner. 90003 Credit: John Boone, UC Davis 90004 90005 90006 Dedicated Breast CT Scanner: 90007 90002 90006 90007 90004 NIBIB is funding research for development of a dedicated breast CT scanner that allows the breast to be imaged in 3D and could help radiologists detect hard-to -find tumors. The scanner produces a radiation dose comparable to that of a standard x-ray mammogram and does not require compression of the breast. In this breast CT scanner, a woman lies prone in a specially designed large table with her breast suspended in a special opening in the scanning bed.The scanner rotates around the breast, without passing through the chest, thus reducing the radiation that would be delivered to the chest in a conventional CT scanner. Click here to read more about dedicated breast CT or listen to a podcast about the scanner. 90012 90005 90006 Reduction in Radiation from Routine CT Scans: 90007 NIBIB put out a call for researchers to submit groundbreaking ideas that will help to radically decrease the amount of radiation used in CT scans. Five new projects are underway from this new funding opportunity, representing creative, innovative, interdisciplinary approaches that would not have been funded otherwise.You can read more about them below: 90012 90005 90006 Customized imaging 90007 90003 90006 Web Stayman, Johns Hopkins University 90007 90003 The amount of radiation required for a CT scan depends on a number of variables, including the size of the patient, the part of the body being scanned, and the diagnostic task at hand. For example, smaller patients require less radiation than larger patients, and scanning a denser part of the body, such as soft tissue near the pelvis, requires more radiation than scanning the lungs.In addition, diagnostic tasks that require high image clarity, such as locating a faint tumor, generally require more radiation. The goal of this project is to modify both the hardware and software of modern CT systems so that the device can adapt the shape, position, and intensity of the x-ray beam to the specific imaging scenario. The research leverages patient-specific anatomical models and mathematical models of imaging performance to direct x-rays where they are needed and, consequently, to avoid or to limit x-ray exposure where it is not needed.This will help maximize imaging performance for specific diagnostic tasks while minimizing radiation exposures. 90012 90005 90006 Constructing tools for researchers 90003 Cynthia McCollough, Mayo Clinic 90007 90003 The goal of this work is to develop resources that enable the research community to easily create and compare new approaches to reducing radiation dose of routine CT scans without compromising diagnostic accuracy. So far, this has entailed creating a library of raw data from patient CT scans that researchers can manipulate to test new approaches, and developing computer-based methods for evaluating new approaches, so that researchers do not have to rely on radiologists, which can be costly and time consuming.Using these assets, researchers have demonstrated that there is considerable potential for radiation dose reduction in CT exams of the abdomen, which are among the highest dose CT exams in common clinical use. 90012 90005 90006 Faster processing 90007 90003 90006 Jeffrey Fessler, University of Michigan 90007 90003 To reduce radiation yet still produce good quality CT images, more sophisticated methods are needed to process the raw data from the CT system. Those advanced methods, called image reconstruction algorithms, can require undesirably long computing times, so they can be used only for some patients currently.The goal of this project is to develop algorithms that are fast enough to allow low-dose CT imaging to be used for every patient.> 90012 90005 90006 An integrated approach 90007 90003 90006 Norbert Pelc, Stanford Medical School 90007 90003 At every stage in the design of CT scanners, there are opportunities to make changes that reduce radiation dose. Because these changes are inter-related, the goal of this project is to take an integrated approach, exploring approaches such as modifying the photon counting detector (the part of the CT scanner that detects x-rays), dynamic x-ray illumination (adjusting the amount of radiation used throughout the duration of a scan), and image reconstruction methods.These will be tested using a table top experimental system. The researchers believe that these combined strategies can lead to as much as 80% reduction in radiation dose compared to today’s typical systems, and also enable higher resolution images. 90012 90005 90006 SparseCT 90007 90003 90006 Ricardo Otazo and Daniel Sodickson, New York University School of Medicine 90007 90003 Investigators at New York University School of Medicine, Brigham and Women’s Hospital, and Siemens Healthineers are working together to develop a new ultra-low-dose CT technique called SparseCT.The key idea behind SparseCT is to block most of the X-rays in a CT scan before they reach the patient, but to do so in a way that preserves all the essential image information. The approach combines a new x-ray blocking device with the mathematics of compressed sensing, which allows images to be reconstructed from reduced datasets. Compression sensing can be likened to filming a movie with a very fast, but low-pixel camera and then using math to convert the image to high-definition quality. 90012 .90000 What is Computed Tomography? | FDA 90001 90002 90003 Conventional X-ray Images 90004 90005 90006 90007 Figure 1: Chest X ray Image 90008 90009 90006 All x-ray imaging is based on the absorption of x rays as they pass through the different parts of a patient’s body.Depending on the amount absorbed in a particular tissue such as muscle or lung, a different amount of x rays will pass through and exit the body. The amount of x rays absorbed contributes to the radiation dose to the patient. During conventional x-ray imaging, the exiting x rays interact with a detection device (x-ray film or other image receptor) and provide a 2-dimensional projection image of the tissues within the patient’s body — an x-ray produced «photograph» called a «radiograph.» The chest x ray (Figure 1) is the most common medical imaging examination.During this examination, an image of the heart, lungs, and other anatomy is recorded on the film. 90009 90006 90013 back to top 90014 90009 90002 90003 Computed Tomography (CT) 90004 90019 90006 90007 Figure 2: Cross-sectional Image of Abdomen 90008 90009 90006 Although also based on the variable absorption of x rays by different tissues, computed tomography (CT) imaging, also known as «CAT scanning» (Computerized Axial Tomography), provides a different form of imaging known as cross-sectional imaging.The origin of the word «tomography» is from the Greek word «tomos» meaning «slice» or «section» and «graphe» meaning «drawing.» A CT imaging system produces cross-sectional images or «slices» of anatomy, like the slices in a loaf of bread. The cross-sectional images (Figure 2) are used for a variety of diagnostic and therapeutic purposes. 90009 90006 90013 back to top 90014 90009 90002 90003 How a CT system works 90004 90033 90006 90007 Figure 3: Patient in CT Imaging System 90008 90009 90038 90039 A motorized table moves the patient (Figure 3) through a circular opening in the CT imaging system.90040 90039 As the patient passes through the CT imaging system, a source of x rays rotates around the inside of the circular opening. A single rotation takes about 1 second. The x-ray source produces a narrow, fan-shaped beam of x rays used to irradiate a section of the patient’s body (Figure 4). The thickness of the fan beam may be as small as 1 millimeter or as large as 10 millimeters. In typical examinations there are several phases; each made up of 10 to 50 rotations of the x-ray tube around the patient in coordination with the table moving through the circular opening.The patient may receive an injection of a «contrast material» to facilitate visualization of vascular structure. 90040 90039 Detectors on the exit side of the patient record the x rays exiting the section of the patient’s body being irradiated as an x-ray «snapshot» at one position (angle) of the source of x rays. Many different «snapshots» (angles) are collected during one complete rotation. 90040 90039 The data are sent to a computer to reconstruct all of the individual «snapshots» into a cross-sectional image (slice) of the internal organs and tissues for each complete rotation of the source of x rays.90040 90047 90006 90013 back to top 90014 90009 90002 90003 Advances in Technology and Clinical Practice 90004 90055 90006 90007 Figure 4: CT Fan Beam 90008 90009 90006 Today most CT systems are capable of «spiral» (also called «helical») scanning as well as scanning in the formerly more conventional «axial» mode. In addition, many CT systems are capable of imaging multiple slices simultaneously. Such advances allow relatively larger volumes of anatomy to be imaged in relatively less time.Another advancement in the technology is electron beam CT, also known as EBCT. Although the principle of creating cross-sectional images is the same as for conventional CT, whether single- or multi-slice, the EBCT scanner does not require any moving parts to generate the individual «snapshots.» As a result, the EBCT scanner allows a quicker image acquisition than conventional CT scanners. 90009 90006 90013 Some Photos Copyright © 2002 GettyImages 90014 90009 90006 90013 back to top 90014 90009 90003 Required Reports for Industry 90004 90072 90039 90003 Content current as of: 90004 90006 90077 12/05/2017 90078 90009 90040 90039 90040 90083 .90000 13. Cone-Beam Computed Tomography: Anatomy 90001 90002 Maxilla and Midfacial Bones 90003 90004 The maxilla and palatine bones form the upper jaw. The maxilla comprises a pyramidal-shaped body and four processes-alveolar, palatine, zygomatic, and frontal. The alveolar and palatine processes articulate in the midline to form the intermaxillary suture between the central incisors, best evaluated on coronal and axial sections. Examine the alveolar process, which forms the bone around the maxillary teeth, along with the maxillary teeth and supporting periodontal structures.In particular, owing to their three-dimensional nature, CBCT scans demonstrate the relationship of the molar and premolar teeth to the floor of the maxillary sinus better than periapical and panoramic radiographs. A common anatomic finding is pneumatization of the alveolar process by the maxillary sinus, which may invaginate between tooth roots (Fig. 13-5). 90005 90006 90007 FIGURE 13-5 Coronal 90008 (A) 90009 and sagittal 90008 (B) 90009 CBCT sections through the maxillary posterior region demonstrating the relationship between the teeth and the maxillary sinus floor 90012 (arrows) 90013.The corticated border of the sinus dips in between the tooth roots. Dilaceration of the mesiobuccal root of the maxillary molar is depicted on the coronal image. 90004 The palatine processes are thick horizontal bony projections that form the anterior three-fourths of the hard palate and the floor of the nasal cavity. The integrity and symmetry of the cortical bony contour are best visualized on coronal sections (see Plates 13-4 and 13-5). Disruption of the hard palate suggests developmental disturbances, such as a cleft palate.Areas of bony protuberances or tori are frequently noted, especially in the midline. Numerous nutrient canals also may be observed perforating the cortical outline of the hard palate on high-resolution scans. 90005 90004 The incisive foramen is located in the midline on the anterior aspect of the palatine process, immediately palatal to the maxillary central incisors (Fig. 13-6; see Plate 13-7). Within this foramen are two lateral canals-the incisive canals or foramina of Stensen-that transmit the terminal branch of the descending palatine artery and the nasopalatine nerve.Occasionally, there may be two additional midline canals-the foramina of Scarpa, which transmit the nasopalatine nerves. The shape and size of the incisive foramen is appreciated on axial sections (see Plates 13-2 and 13-3). There is considerable variation in the size of the nasopalatine canal and incisive foramen. It is important to differentiate between a large incisive foramen and an incisive canal cyst because the latter can cause localized dilation of the canal or widening of the incisive foramen and may cause displacement of teeth (see Chapter 21).90005 90018 90007 FIGURE 13-6 90008 A 90009 and 90008 B, 90009 Sagittal CBCT sections through the midsagittal plane showing the course of the nasopalatine canal 90012 (yellow arrow) 90013 and the opening of the incisive foramen 90012 (white arrow) 90013. Note /> Only gold members can continue reading. Log In or Register to continue .90000 Cone Beam Computed Tomography in Orthodontics 90001 90002 1. Introduction 90003 90004 The key of a successful orthodontic treatment is an accurate diagnosis, growth evaluation and treatment planning. Diagnostic records for an orthodontic treatment planning generally begin with history and intraoral and extraoral examination of the patient. Dental casts, intraoral and extraoral photographs are also routine diagnostic materials. Imaging is a necessary diagnostic tool in the practice of orthodontics.For radiographic evaluation, panoramic radiograph, periapical views, upper occlusal radiograph and lateral cephalometric radiograph are obtained if indicated. Imaging should answer the questions that can not be solved clinically. By using radiographic examination, it is possible to confirm or rule out clinical findings [1]. 90005 90004 In recent years, orthodontists have begun to use three-dimensional (3D) cone beam computed tomography (CBCT) images to overcome the inadequateness of two-dimensional (2D) radiographic records.When computed tomography was first introduced into the dental field, because of the high radiation dose, it is not preferred for orthodontic diagnosis. The technology has been evolving ever since, resulting in a reduction in radiation dose and relatively low cost of CBCT systems, so they become popular to visualize the craniofacial complex in three dimensions. 90005 90004 In some studies, it has been suggested that different options for orthodontic treatment plans in some specific cases may change due to use of CBCT [2-4].Orthodontists should know how to use the radiographic records and what they offer, before deciding which tool they will use [1]. 90005 90002 2. Advantages and disadvantages of using CBCT in orthodontics 90003 90004 Although there has been considerable interest in using CBCT as a part of routine orthodontic management, diverse results about the advantages, disadvantages and indications were noted in the literature. 90005 90004 The review of recent literature reveals some advantages [1, 5-15] and disadvantages [16-20] as following: 90005 90016 2.1. Advantages 90017 90018 90019 90004 Accuracy of image geometry is increased, and real size 3D image is obtained by CBCT. Unlike lateral cephalometric radiographs, CBCT image is more similar to the patient, more accurate and distortion-free. 90005 90022 90019 90004 It eliminates the magnification, overlapping and distortion of structures. 90005 90022 90019 90004 It is possible to assess the image from the three planes. 90005 90022 90019 90004 CBCT images allow to make localized and specific transversal cuts to assess areas of clinical interest.90005 90022 90019 90004 For a proper diagnosis and treatment planning, sometimes temporomandibular, posteroanterior cephalograms, periapical, occlusal and bite-wing radiographs are also required besides the routine panoramic and lateral cephalometric examination. But, by using CBCT technology, it is possible to produce several types of radiographic images and to construct study casts from a single scan. 90005 90022 90019 90004 The reorientation of the images, on the contrary to the lateral cephalometric radiograph, is possible.90005 90022 90019 90004 The ease of landmark identification and high precision of superimposed images have been reported. 90005 90022 90019 90004 By the use of CBCT, less variability and more reproducibility of transverse measurements were demonstrated compared to conventional 2D. CBCT images were reported to be more reliable than posteroanterior cephalograms and offer an unobstructed view for diagnosis of maxillary transverse discrepancies. 90005 90022 90019 90004 The unerupted tooth sizes, bone dimensions and even soft tissue anthropometric measurements can be assessed precisely by CBCT.90005 90022 90019 90004 The fine adjustment of the head position is not essential for CBCT. 90005 90022 90019 90004 The use of CBCT in orthodontics greatly enhances evaluation of impacted canines and offers comprehensive information. 90005 90022 90019 90004 The detection of root resorption is reported to be highly accurate with CBCT scanners. 90005 90022 90019 90004 An occlusal view of the maxilla from CBCT can be used for the customized transpalatal arch design. This might prevent interfering of the wire to the path of eruption of impacted tooth.90005 90022 90071 90016 2.2. Disadvantages 90017 90018 90019 90004 The amount of generated radiation is the biggest controversy about the use of CBCT in dental imaging. Although the radiation dose of the CBCT is lower than the medical spiral CT, it is still higher than that of a 2D cephalogram. 90005 90022 90019 90004 Difficulty in differentiating various soft tissues in the image due to the poor low-contrast resolution compared to medical CT is one of the disadvantages. 90005 90022 90019 90004 An adequate method to digitize and analyze 3D radiographic images is not still improved.90005 90022 90019 90004 The lack of 3D standard population norms has also restricted CBCT from routine orthodontic use. 90005 90022 90019 90004 Landmark identification on coronal, sagittal and axial views of CBCT is more time consuming to carefully select the best slice. 90005 90022 90019 90004 The diagnostic accuracy for caries detection with CBCT is less than with conventional periapical radiographs. 90005 90022 90071 90002 3. The usage of CBCT in orthodontics 90003 90004 Many orthodontists interested in using CBCT during their routine diagnosis and treatment planning because of the additional diagnostic information.This brings the risk of unnecessary ionizing radiation. So, it is mandatory to determine exact indications for the use of CBCT in orthodontics. 90005 90016 3.1. Impacted and transposed teeth 90017 90004 Tooth impaction is a commonly observed dental anomaly which needs orthodontic treatment. The most frequent impacted teeth were mandibular wisdom teeth, which were followed by maxillary and mandibular canines [21]. Radiographic examinations play a more critical role than clinical examination especially in the initial diagnosis and treatment planning of impacted teeth.For several years, radiographic evaluation of these teeth was done by using panoramic, periapical, occlusal or lateral cephalograms. These conventional two dimensional radiographs are inadequate in accurately visualizing the location, angulation, spatial position and relationships of the impacted tooth in three dimensions. So, the most justified indications for the use of CBCT in orthodontics are the existence of impacted and transposed teeth (Figure 1a-c). 90005 90108 Figure 1. 90109 90004 (a) Panoramic view of a maxillary impacted canine.Note that in this case, FOV was restricted only to maxilla. (B) Determination of vestibular location of a maxillary impacted canine. (C) Evaluation of proximity between impacted canine and root of lateral incisor by CBCT. 90005 90004 For the management of the impacted teeth, CBCT enhances the ability to localize these teeth accurately, evaluate their proximity to other teeth and structures, determine the alveolar width and follicle size, the presence of pathology and assess root resorption of adjacent teeth, assist in planning surgical access and bond placement, besides determining optimal direction for the extrusion of these teeth into the oral cavity [22-25].In particular, for impacted teeth, if exposure or forced eruption is planned, it would be possible to determine not only the position of tooth and dilacerated root but also the alveolar boundary conditions. Additionally, it would be much easier to prepare the space needed for the impacted tooth as it is possible to obtain a more accurate size from CBCT images. 90005 90004 Haney et al. [26] reported an approximate 20% lack of agreement among clinicians on the location (palatal versus labial) of the tooth tip between the routine 2D radiographs and 3D CBCT images.Also large differences in treatment approaches were demonstrated when the two imaging methods were compared [27]. On the other hand, in another study, it was reported that the determination of canine position was not significantly different when using panoramic and CBCT systems [3]. 90005 90004 Using CBCT improves the clinician confidence in diagnosis and treatment plan as it is helpful in defining the surgical access site, bond position and in designing mechanics [25, 26]. The orthodontists have a different perception of localization and can determine the shortest way for the impacted tooth in three planes of space while avoiding damage to neighboring teeth.90005 90004 In some studies, it was suggested that orthodontic treatment planning for impacted tooth showed no differences when using 2D- or 3D-based information. On the contrary, findings of some other studies showed that orthodontists changed their treatment planning derived from conventional radiographs for 25% of the impacted teeth when they viewed CBCT images [26, 28]. Alqerban et al. [4, 29] concluded that CBCT allows clinicians to obtain 3D images with visualization of craniofacial structures and significantly increases the orthodontists ‘confidence level, with more information on canine localization and detection of possible root resorption on adjacent incisors [30].90005 90004 When the impacted tooth did not move, CBCT is indicated. Becker et al. [31] reported that invasive cervical root resorption is a rare insidious and aggressive form of external root resorption and an overlooked cause of failure of orthodontic resolution of impacted canines. 90005 90004 CBCT minimizes superimposition artifacts and provides superior visualization of roots [24, 32]. In extraction cases with an impacted tooth, it is a much more important to decide which tooth to extract, a tooth with a resorbed root or a healthy premolar? Using CBCT images will contribute to a logical clinical outcome, as it provides superior information on root resorption.90005 90004 Overall, it could be considered to increase efficiency and enhance success rates for the treatment of impacted teeth when the treatment and biomechanics are customized by using CBCT [33]. 90005 90004 Field of view (FOV) must be determined according to the needs of the case. If the only problem is an impacted tooth, it would be logical to localize the FOV as the impacted tooth, adjacent teeth and surrounding alveolar structure. In fact, in a recent study, Wriedt et al. [30] recommended small volume FOV CBCT for impacted maxillary canines if the canine inclination on a conventional 2D panoramic radiograph exceeds 30 ° relative to a perpendicular midline, when adjacent root resorption is suspected, and / or when canine root dilaceration is suspected on conventional panoramic radiographs.But if an orthognathic surgical treatment plan is predicted, cephalometric and panoramic radiograph need must be considered while determining FOV. It is advisable to refer the patient to an oral and maxillofacial radiologist with a note including clinically significant findings and request a report on the region of interest [27]. 90005 90004 Maxillary lateral incisor root resorption is most commonly associated with canine impaction. It often remains asymptomatic, limiting early diagnosis. However, early diagnosis is important, because the presence or absence of root resorption will determine the treatment strategy.Furthermore, advanced root resorption can make treatment impossible [34]. Improvement in diagnostic measures for early detection and prevention is therefore essential for ensuring correct treatment, and it might also reduce treatment time, complexity, complications and costs. It has been suggested that by using 3D images, overlapping of structures can be avoided. 90005 90004 Dental transposition represents a multifactorial condition. In the etiology of transposition, both genetic and environmental factors play an important role [35].For the diagnosis and treatment planning of transposed teeth, several significant variables can be derived from CBCT imaging, especially, critical when deciding whether patient requires extraction or not. So, it would be much easier to evaluate adequately the quality and shape of teeth, location of roots and limitations of the alveolar boundary conditions around the transposed teeth by using CBCT. Kapila et al. [28] recommended to be selective about which cases may benefit from CBCT scans for assessing boundary conditions.Cases with compromised periodontal or gingival conditions, patients with narrow alveolar bone in which it would be critical to manage buccolingual displacements or angulations of teeth, and cases who need shifting position of the teeth are listed as cases that will benefit from CBCT scans. 90005 90016 3.2. Supernumerary teeth 90017 90004 A supernumerary tooth may closely resemble the teeth of the group to which it belongs [36]. In supernumerary cases, radiographic examination aims to determine the localization and the morphology of the supernumerary teeth.As it is critical to decide which teeth to be extracted and which teeth to be retained, CBCT helps to precisely evaluate the position and morphology of these teeth. It is also possible to detect any contact between the supernumerary teeth and adjacent teeth and to evaluate their relation with other anatomical structures. The information obtained from CBCT images also facilitates the determination of the optimal surgical access to these teeth in order to minimize harm to adjacent teeth and to surrounding tissue [37] (Figure 2).90005 90108 Figure 2. 90109 90004 Evaluation of position of a supernumerary tooth and impacted incisor and their relation with neighboring structures. 90005 90016 3.3. Root resorption 90017 90004 Root resorption is a condition occurs in response to a variety of stimuli resulting in a loss of dentin, cementum or bone [36]. Panoramic radiographs have a week diagnostic efficacy in determining external root resorption. So, root resorption has traditionally been evaluated by periapical radiographs.Nevertheless, in recent years, it is suggested that CBCT can detect precise images of small root defects with a greater sensitivity and specificity compared to 2D radiographs [3, 24]. In a meta-analysis, Yi et al. [38] reported that CBCT is superior to periapical radiographs in the accuracy of diagnosing external root resorption. They emphasized that periapical radiographs provide limited information of external root resorption in the buccal and lingual root surface. 90005 90004 External root resorption of maxillary lateral incisor is a common finding that associates with canine impaction.Early diagnosis is difficult as it is asymptomatic and advanced root resorption makes the treatment planning more complex. In a study evaluating efficacy of CBCT for the diagnosis of root resorption associated with impacted canines, improved detection rates of root resorption (63%) were reported [39]. By using CBCT, it is possible to visualize of root resorptions on buccal and lingual surfaces. This might be critical for the extraction decision during treatment planning. In another study, it was suggested that the combination of thin slices and high resolution caused overestimation of the cavities for moderate root resorption cases [3].90005 90004 The main problem is to decide how and when a clinician justify taking CBCT scan when a patient has undergone root resorption. Yi et al. [38] suggested that patients with clinically suspected root resorption be first evaluated by periapical radiographs. If positive results are obtained, for further examination, CBCT should be considered. 90005 90004 Alqerban et al. [10] reported that all CBCT systems used in their study showed high accuracy in the detection of root resorption, and there was no significant difference among CBCT systems in the detection of the severity of root resorption.Limitations of using CBCT for external root resorption are the detection of small resorptions in the apical third and the high dose of radiation required [3]. 90005 90016 3.4. Evaluation of root angulation and length 90017 90004 CBCT imaging becomes a preferred method for diagnosis by orthodontists because of its three dimensional rendering capability. Root position and morphology are critical issues for an orthodontist as it may affect the final occlusion. Root anatomy, such as short or dilacerated, is a determinant factor for the amount and direction of a tooth movement.Furthermore, because of the concerns about external root resorption, orthodontists need to get precise measurements of root angulation and length before treatment. Using CBCT images also provide detailed information about dysmorphic roots. Root positioning and morphology might be indicators of a disease. Of course, all root anomalies are not identical, but when supported with genetic testing, CBCT imaging will be helpful in interpreting anomalous root morphology in syndromic cases [40]. 90005 90016 3.5. Tooth-bone relationship 90017 90004 In bimaxillary protrusion cases, Class 3 patients with an initial symphysis bone width, cases with preexisting periodontal disease, after maxillary expansion treatment, CBCT provides valuable information about tooth-bone relationships, and it might reduce the risk factor for dehiscence. While assessing deficiencies of buccolingual thickness in the alveolar ridge of patients subjected to critical tooth movement, high resolution and a limited FOV is recommended [41].90005 90016 3.6. Cleft lip and palate (CLP) cases 90017 90004 Patients with CLP are treated by interdisciplinary teams from infancy until adulthood. Several types of surgical procedures are used to reconstruct the anatomy of the alveolar ridge, dentofacial region, lips and nose. The SEDENTEXCT Consortium stated, in regard to the radiation dose, that «the application of CBCT in cleft lip and palate patients was found to be the simplest to support» in dentistry [42]. However, in a recent systematic review, it was suggested that further investigation is necessary to determine the influence of this new 3D facial imaging modality on treatment planning, treatment outcome and treatment evaluation.90005 90004 The preoperative CBCT may provide reliable estimates on how much expansion and graft material will be needed, aid in appropriate selection of an autogenous graft donor site before surgery and enable the visualization of the three-dimensional morphology of the bone bridge, the relationship between the bone bridge and roots of the neighboring teeth. For alveolar bone graft success, determination of the buccal-palatal width of the bone in CLP cases, the use of CBCT is recommended [43] (Figure 3).Pharyngeal space, the results of bone grafting, and the effect of nasoalveolar molding can be evaluated with a post-treatment CBCT. 90005 90108 Figure 3. 90109 90004 Preoperative CBCT view of a CLP case showing the graft site. 90005 90016 3.7. Temporomandibular joint (TMJ) morphology and pathology contributing to malocclusion 90017 90004 The changes in the size, form and special and functional relationships of the TMJ components might cause pathological TMJ conditions. TMJ disorders which occurred during active growth period might alter jaw, tooth positions and occlusion.Even though signs and symptoms of disturbances in the masticatory system are common, understanding the cause can be very complex. A proper diagnosis is possible, if only a through history and examination were achieved. Various types of imaging techniques can be used to gain additional information regarding the health and function of TMJs. CBCT is indicated for orthodontic cases that require analysis of TMJ bone components accompanied by signs and symptoms [44, 45]. One of the greatest advantages of CT scan is evaluating the condyle-disk relationship [46].In comparison with panoramic radiograph and linear tomography, CBCT proves more accurate in diagnosing erosion of the condyle [47]. Soft tissue imaging is possible, but bony tissues are best imaged with CT scans [48]. As magnetic resonance imaging enables visualizing the non-mineralized soft tissues, it is preferable for the diagnosis of internal derangements of TMJ. However, it is not possible to observe dynamic joint movements. 90005 90004 Besides the evaluation of TMJ disorders, CBCT has been used to evaluate the condylar changes after orthodontic treatment.It allows volumetric evaluation of TMJ and provides better landmark identification on curved surfaces like condyle. Literature review showed that CBCT evaluation was preferred to determine respond of TMJ to mandibular advancement [49] or extraction treatment [50] and effects of the distraction splint therapy in mandibular asymmetry cases. 90005 90016 3.8. Airway morphology and obstructive sleep apnea (OSA) 90017 90004 Sleep-disordered breathing is a spectrum of conditions with abnormal respiratory pattern, and OSA is the severe end of that spectrum.Orthodontics takes place in the management of OSA by using mandibular advancement appliances and by planning orthognathic surgery in these cases. It is also crucial to evaluate the dimensional changes in the nasopharyngeal area and airway obstruction in CLP [51]. Until recent years, lateral cephalometric radiography was used for the evaluation of the upper airway. But, changes which occur in the transverse dimension can not be visualized. Three-dimensional analysis and evaluation of airway have got a significant attention in the literature.CBCT allows orthodontists to measure cross-sectional area, minimum cross section and total volume of the patient’s airway accurately. Also, it has been used to investigate the effects of orthodontic treatments and orthognathic surgery on airway dimensions. 90005 90004 Studies of the upper airway based on CBCT scans are considered to be reliable in providing important information about the morphology of the pharyngeal airway; however, they have limitation in distinguishing different types of soft tissues [52].Variations in airway dimensions and morphology due to patient’s swallowing movement and head posture are also among the limitations of this technique [53]. 90005 90016 3.9. Maxillary transverse dimension and maxillary expansion 90017 90004 In the treatment of transverse maxillary deficiencies, it is important to assess transverse dimension as early as possible and accurately diagnose the need for transverse maxillary expansion using proper diagnostic tools. Before CBCT, post-treatment skeletal changes on patients treated with RME were measured on dental casts, lateral and posterior-anterior cephalometric and occlusal radiographs.Researches to date on rapid maxillary expansion have focused on determining treatment outcomes like dental tipping, alveolar bone bending, skeletal expansion and soft tissue changes, rather than the benefits of CBCT in diagnosis and treatment planning. Nowadays, it is claimed that CBCT images appear to be more reliable than posteroanterior cephalograms, offer an unobstructed view for the assessment of transversal intermaxillary discrepancies and provide much greater resolution and minimal image distortion [15].However, the radiation dosage and its effect on growing patients must be taken into account. 90005 90004 The mid-palatal suture becomes more fused after the completion of the adolescent growth spurt [54], as prediction of mid-palatal suture maturation is possible by using CBCT [55]. It is a reliable diagnostic tool, while planning surgically assisted rapid maxillary expansion (SARME) in skeletally mature patients or using bone-borne devices, which have recently gained popularity. It is possible to determine treatment outcomes of SARME and also permits the detection of the complications, such as tooth tilting of the anchoring teeth and bone fenestration due to periodontal stress [56].90005 90016 3.10. Temporary anchorage device (TAD) placement 90017 90004 In recent years, TADs are considered as a prerequisite for the resistance of unwanted tooth movements during the treatment of various orthodontic problems without patient compliance. The most common indications for treatment with TADs are molar protraction followed by indirect skeletal anchorage for space closure, intrusion of supraerupted teeth, intrusion of anterior to manage anterior open bite, anterior en-masse retraction, molar uprighting, intrusion of maxillary cant, molar distalization , traction on impacted canine, and attachment for protraction facemask.CBCT images can be helpful to anchor the miniscrew and miniplate securely in the surrounding bone and to visualize neighboring structures for avoiding damage or complications during TAD placement and be useful in identifying optimal site location (Figure 4). 90005 90108 Figure 4. 90109 90004 Planning and preparation of TAD (zygomatic skeletal anchorage) on a 3D model obtained from CBCT before surgery. 90005 90004 CBCT technology enables us to evaluate the interradicular distance and thickness, transverse bone thickness, bone density and thickness, cortical bone dimensions and quality.Even though anterior palate offers the greatest bone thickness, Holm et al. [57] recommended a CBCT evaluation for maximum screw length, as there is considerable variation of bone thickness between individuals. Before placing a miniscrew by using CBCT, it is also possible to define even cranial and caudal boundaries, besides alveolar boundary conditions, and eliminate the risk of bone and root perforations. Surgical guides fabricated using CBCT images will help to avoid possible root and maxillary sinuses damage.Finite element analysis constructed using CBCT will also guide the evaluation of mechanical advantages or disadvantages of the orthodontic appliances with TADs by simulating stress distribution. 90005 90004 There are several factors that affect the stability and success rate of TADs. If cortical bone thickness is less than 1 mm, primary stability may not be achieved, and the TAD may loosen during orthodontic treatment [58]. Evaluation of cortical bone quantity and quality is also critical for long-term stability.With finite element analysis, it has been shown that root contact is also one of the factors that can cause loss of miniscrew stability [59]. The information gathered from CBCT will be determinant for some of these factors, such as the dimension and insertion angle of the miniscrew, the insertion procedure, the depth of the screw insertion and insertion torque [38, 57, 60]. 90005 90004 In some cases, routine panoramic, lateral and frontal cephalometric radiographs may not provide all information needed to optimize the location of a miniscrew placement.However, it should be kept in mind that in regions with a high bone quality, such as paramedian palate and palatal region, lateral cephalometric radiographs are usable to determine the location of TADs. Therefore, it is not necessary to take a CBCT in all cases [61]. 90005 90004 It is recommended to use the smallest possible FOV unless the CBCT is needed for the diagnosis of another condition in which case a large FOV may be preferred [60]. 90005 90016 3.11. Dentofacial deformities and craniofacial anomalies 90017 90004 Evaluation of changes in the craniofacial region during growth and with treatment using lateral cephalograms makes a great contribution to the science of orthodontics.However, in recent years, researches discussed the validity of evaluating a 3D craniofacial structure in a 2D plane. CBCT imaging can provide valuable information about dentofacial deformities and craniofacial anomalies, like facial asymmetry which affects three dimensions of the face, and it can be used to simulate virtual treatment plans for orthopedic corrections, orthognathic surgeries and distraction osteogenesis. By capturing images and analyzing the craniofacial hard and soft tissues and by generating virtual patient models, CBCT imaging permits the clinicians to reposition and reconstruct craniofacial structures (Figure 5a, b).90005 90108 Figure 5. 90109 90004 (a) 3D view of a case with Golden Haar syndrome. Note the asymmetric growth of left and right condyles. (B) 3D evaluation of mandible and condyles in this case. 90005 90004 Several studies were conducted to determine reference planes, to develop cephalometric analysis, to evaluate the accuracy of these measurements, to establish the mean normality values and to assess the differences of gender and ethnic groups for 3D evaluations [62]. Besides morphological analysis, these images are used to evaluate the spatial relationship of the neighboring structures.CBCT technology enables carrying out the model surgery. So, computer assisted orthognathic surgery permits the design and fabrication of the occlusal surgical splints. By using virtual models, constructing anatomically grafts and correct replacement can be achieved (Figure 6). The data obtained from CBCT provide a better prediction of soft tissue response to the changes in the hard tissue after orthognathic surgery [63]. In the literature, CBCT is recommended for the assessment of preoperative orthodontic decompensation of maxillary and mandibular incisors [64].This is an additional information from CBCT that is taken for orthognathic surgery planning, and it could not be one of the main purpose of using CBCT. Furthermore, CBCT proves a good method to assess TMJ after orthognathic surgery, particularly when there is considerable potential for resorption of the condyle [14]. 90005 90108 Figure 6. 90109 90004 Presurgical 3D model of a case with Crouzon syndrome obtained from CBCT. 90005 90016 3.12. Treatment outcomes 90017 90004 Taking CBCT at the end of orthodontic treatment is a controversial issue.However, it must be taken into consideration that studies on response to treatment can help elucidate clinical questions on variability of outcomes of treatment. There are studies assessing treatment outcomes of orthognathic surgery, maxillary expansion, bone grafting and several orthopedic appliances. A review of literature showed that jaw and teeth relationships, soft tissue, hyoid bone position, pharyngeal airway dimensions and morphology were evaluated after orthodontic and surgical treatments.To facilitate the evaluation of treatment outcomes, superimposition methods for CBCT images were also offered [28]. 90005 90016 3.13. Evaluation of cervical vertebral maturation (CVM) 90017 90004 Skeletal maturation of patients is an important factor while planning orthodontic treatment. Hand-wrist and CVM methods were used for assessing the adolescent growth peak. It is suggested that the CBCT images may be useful for estimates of skeletal maturation, although they should not be used solely for that purpose [65].Shim et al. [66] claimed that the estimate of maturation stages of the cervical vertebrae on CBCT provided a reliable evaluation of pubertal growth support and strongly positive correlations with lateral cephalograms and hand-wrist radiographs. 90005 90002 4. Radiation dose 90003 90004 Radiation dose depends on the CBCT scanner’s specifications, milliampere setting, peak kilovoltage (kVp), voxel size, sensor sensitivity and number of images obtained, the time of scanning, and FOV. It is recommended to apply the 3D evaluation when the use of CBCT can be justified.Clinicians should always keep in mind that the radiation exposure to a human being should be kept «As Low As Reasonably Achievable» (ALARA) principle. 90005 90004 SEDENTEXCT project guidelines include a variety of topics, like justification, referral criteria, optimization, training, quality assurance and staff protection aspects [67]. Justification of using CBCT in dentistry can be considered if only a patient history and clinical information are available, if additional new information is expected, and if 2D radiographs are inadequate for diagnosis.The orthodontist should weigh the potential benefits of a CBCT against the chance of causing cancer for each patient. The chance may be small, but it is never negligible. 90005 90004 To reduce the patient dose, the smallest available volume size should be preferred. kVp and mAs of CBCT used in dental and maxillofacial region vary in a wide range and patients ‘doses varies considerably. It is recommended to standardize exposure parameters in dental and maxillofacial CBCT for each imaging task [68].Gamache et al. [7] suggested that the total radiation exposure from CBCT scans can be reduced by while maintaining adequate image quality using low kV and moderate-to-high mA settings rather than the manufacturer-recommended settings. 90005 90004 Voxel size should be determined according to the purpose of the exam. When voxel dimension decreases, a better spatial resolution will be achieved, but the radiation dose will be increased [70]. Voxel sizes of 0.3-0.4 mm should be preferred if there is no need for a high level of detail [41].90005 90004 Using child dose is offered because effective doses are higher compared with adults if exposure factors are not adapted. In a study on estimation of pediatric organ and effective doses from dental CBCT in 2012 it was reported that the average effective doses to the 10-year-old and adolescent phantoms were 116 and 79 mSv, respectively, which are similar to adult doses. So, the authors concluded that dental CBCT examinations on children should be fully justified over conventional X-ray imaging due to the higher radiosensitivity of children and that dose optimization by FOV collimation is particularly important in young children [69].FOV should be restricted as much as possible [42]. So, the examination should include only the areas of interest in order to minimize radiation dose and ALARA principle must be followed. Repeated CBCT examinations should be avoided. The patient must be informed, and consent of the patient or parents must be obtained. 90005 90004 Technical properties of CBCT units were given inadequately in several studies. To make a comparison based on effective dose between studies, these properties must be reported and more evidence base studies on effective dose and image quality relation are still needed [70].90005.